kmp匹配字符串

kmp算法常用于优化字符串匹配，例如下面的问题：

有一个字符串a = “BBC ABCDAB ABCDABCDABDE”，我想知道，里面是否包含另一个字符串b = “ABCDABD”

一般的做法是循环比较。

func contain(a string, b string) bool {
  for i := 0; i < len(a); i++ {
    k := i
    for j := 0; j < len(b); {
      if b[j] == a[k] {
        if j == len(b)-1 {
          return true
        }
        j++
        k++
      } else {
        //匹配失败
        j = 0
        break;
      }
    }
  }
  return false
}

可以看到耗时O（n*m）,每一次失败都是从头逐个比较，特别对于ABCDAB多次重复匹配，kmp算法通过配置部分匹配表，减少这些重复匹配操作，从而达到优化效果。

KMP算法的精髓在于对已知信息的充分利用，理解kmp算法首先要了解一些概念：

1. 字符串前缀，真前缀，后缀，真后缀，及前缀函数

举个例子，如字符串 ABCDABD，首先，不考虑空字符

前缀有A,AB,ABC,ABCD,ABCDA,ABCDAB,ABCDABD

真前缀有A,AB,ABC,ABCD,ABCDA,ABCDAB

同理可以理解后缀，真前（后）缀就是指不包含自身的前（后）缀

真后缀为BCDABD,CDABD,DABD,ABD,BD,D

“真前缀”指除了最后一个字符以外，一个字符串的全部头部组合；

“真后缀”指除了第一个字符以外，一个字符串的全部尾部组合。

这里指的是真前缀后缀
   －　"A"的前缀和后缀都为空集，共有元素的长度为0；
　　－　"AB"的前缀为[A]，后缀为[B]，共有元素的长度为0；
　　－　"ABC"的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度0；zh
　　－　"ABCD"的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为0；
　　－　"ABCDA"的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为"A"，长度为1；
　　－　"ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为"AB"，长度为2；
　　－　"ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为0。

前缀函数next[]是指某个字符串的最长真后缀同时也是它的前缀的子串长度。

array = {A, B, C, D, A, B, D}

next  = {-1, 0, 0, 0, 1, 2, 0}

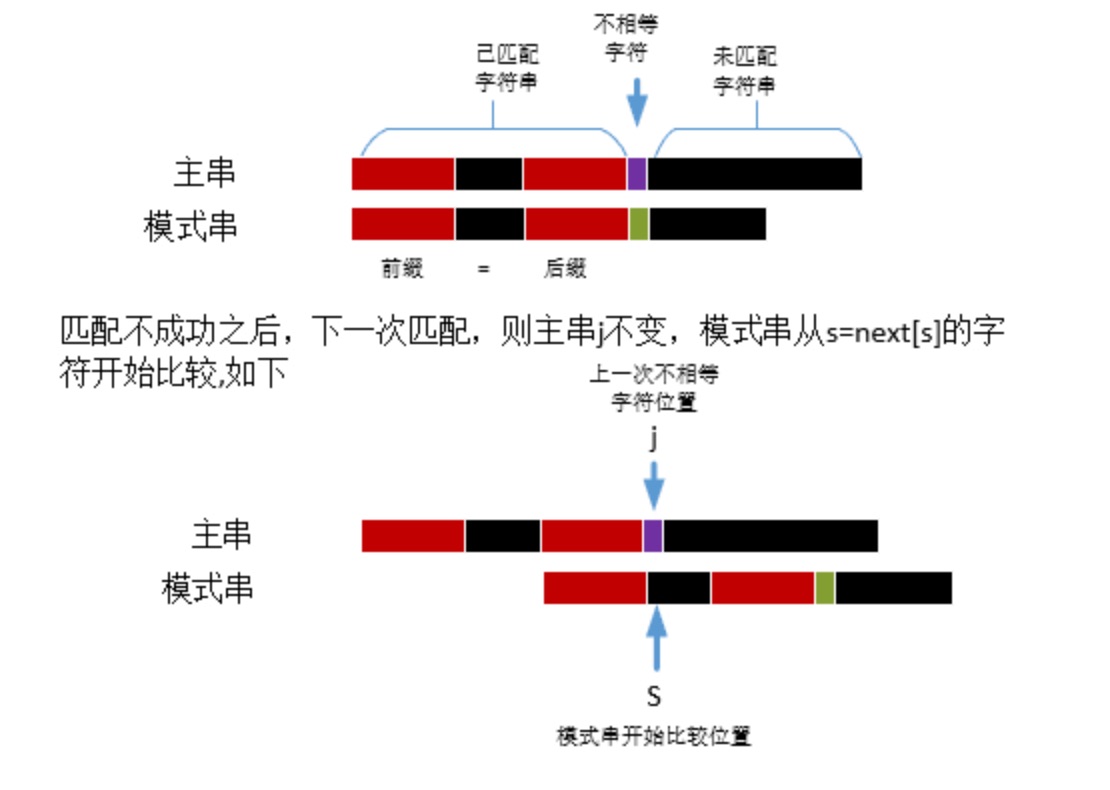
“部分匹配”的实质是，有时候，字符串头部和尾部会有重复。比如，”ABCDAB”之中有两个”AB”，那么它的”部分匹配值”就是2（”AB”的长度）。搜索词移动的时候，第一个”AB”向后移动4位（字符串长度-部分匹配值），就可以来到第二个”AB”的位置.

/**
部分匹配表
 */
func prefixFunction(str string) []int {
  sLen := len(str)
  prefix := make([]int, sLen)

  i := 0
  for j := 1; j < sLen-1; j++ {

    if str[j] == str[i] {
      i++
      prefix[j] = i
    } else {
      i = 0
    }
  }

  return prefix
}

/**
转移数组
 */
func obtainMoveFromPrefix(prefix []int) [] int {
  sLen := len(prefix)
  move := make([]int, sLen)
  move[0] = -1;
  for i := 0; i < sLen; i++ {
    if i == 0 {
      move[0] = -1;
    } else {
      move[i] = prefix[i-1]
    }
  }
  return move
}


func contain(a string, b string) bool {
  m, n := len(a), len(b)
  move := obtainMoveFromPrefix(prefixFunction(b))

  j := 0
  for i := 0; i < m; i++ {

    //有匹配的字符
    for j > 0 && b[j] != a[i] {
      j = move[j]
      if j < 0 {
        j = 0
      }
    }
    if b[j] == a[i] {
      j++
    }
    if j == n {
      return true
    }
  }

  return false

}

参考文章：

kmp算法-wiki

字符串匹配的KMP算法

KMP 算法详细解析

从有限状态自动机的角度理解KMP算法