float_and_double

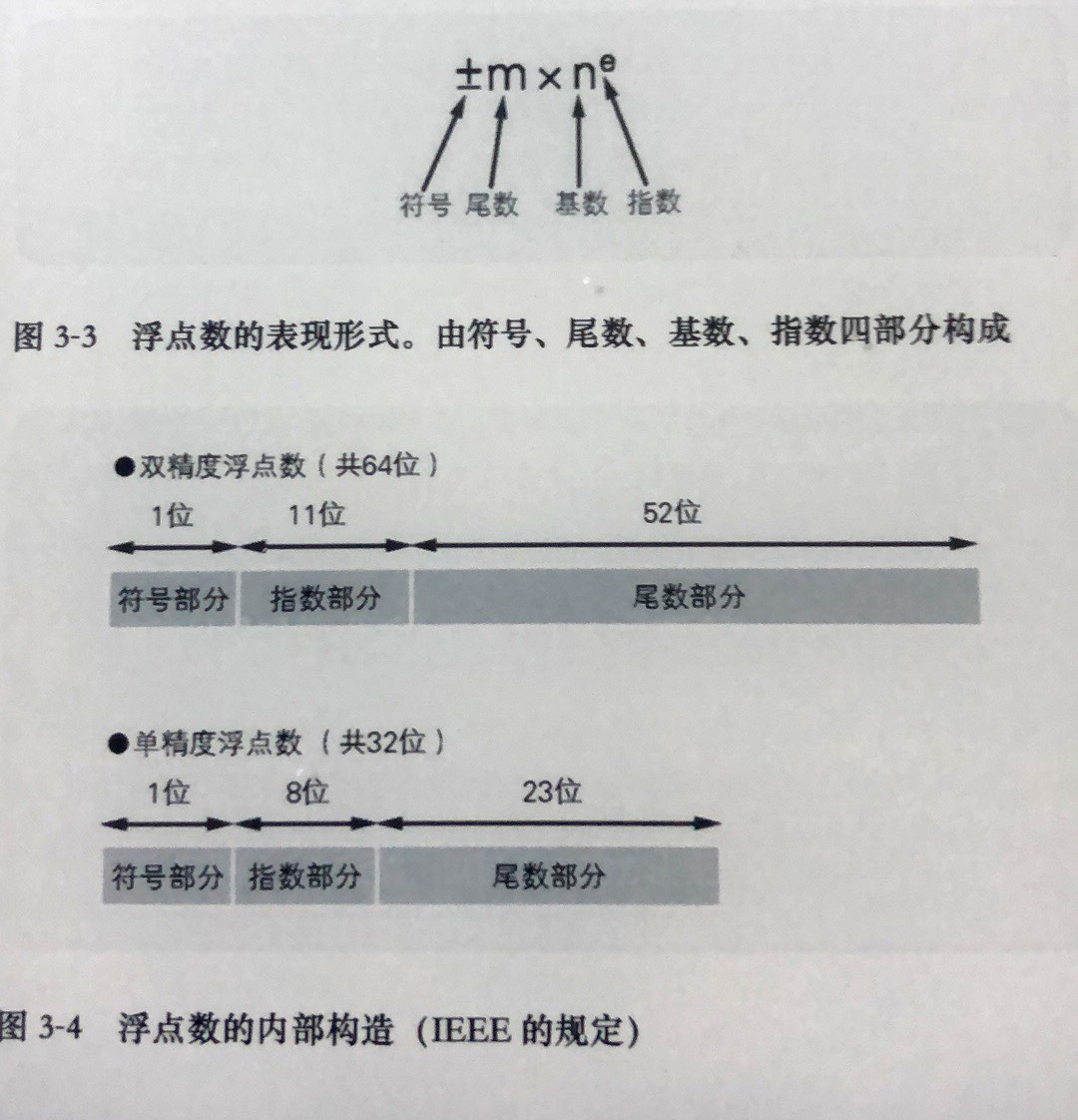
浮点数是指用符号，尾数，基数和指数这四部分来表示的小数。因为计算机内部使用的是二进制数，所以基数自然是2。

来源

CPU中的二进制数据（小数篇）

计算机浮点数规格化表示

单精度与双精度是什么意思，有什么区别？

浮点数

• 双进度 64 位,8byte

• 单精度 32 位,4byte

`

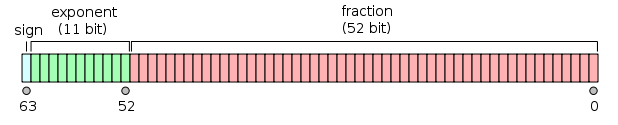
1. IEEE 754標準規定：非正規形式的浮點數的指數偏移值比正規形式的浮點數的指數偏移值小1。例如，最小的正規形式的單精度浮點數的指數部分編碼值為1，指數的實際值為-126；而非規約的單精度浮點數的指數域編碼值為0，對應的指數實際值也是-126而不是-127。實際上非正規形式的浮點數仍然是有效可以使用的，只是它們的絕對值已經小於所有的規約浮點數的絕對值；即所有的非規約浮點數比規約浮點數更接近0。規約浮點數的尾數大於等於1且小於2，而非規約浮點數的尾數小於1且大於0

2. 小数部分是原十进制数值变为二进制后再经过规格化，规格化后省去唯一的整数1之后剩下的0.0100000 00000000 00000000写进去的。

3. 指数部分是由指数实际值-3再加上固定值（这里取IEEE754标准的固定值2**（e-1）-1,e为储存指数的比特长度，在这里是8 bit）(单精度时指数偏移度为127，目的是为了同时可以表示正和负的指数，即00000000-11111111分别对应-127 — 128)。

   # 十进制运算
   0.15625-(1.0/8)-0-(1.0/32) = 0
   # 因式分解,用二的倍数表示
   0.15625=(1.0/8)+0+(1.0/32)
   # 转为二进制
   0.15625=(1)*(0+0.00101)=(1)*(1+0.01)x2^(-3)
   # 二进制下小数位为0.01
   # 尾数为0100 0000 0000 0000 0000 000
   # 指数 -3
   (-3)-(-127)=134 => 0b0111_1100
   
   

一个32位单精度浮点数-3.75表示的例子:

#首先转化为2进制表示
−3.75=−(2+1+1/2+1/4)=−1.111×2^1
#整理符号位并进行规格化表示
−1.111×21=(−1)(1)×(1+0.1110 0000 0000 0000 0000 000)×2^1
# 尾数为1110 0000 0000 0000 0000 000
# 指数为1-127=128=0b10000000

精度

浮点数的尾数是二进制的,转化之后,有一些数无法表示,这也是精度丢失的原因.